Fractal dimension and size distribution characteristics of ultra-high-molecular-weight polyethylene wear particles in condition of artificial knee joint simulator
Introduction
Wear debris is formed on the wear surface of the material. In the detection of oil debris particles, the wear state of the machine can be judged according to the change of the shape of wear debris. As a typical friction pair, the artificial joints also generate a large number of wear particles due to the wear movement, which has become the direct cause of the wear debris disease called in clinical (1-5). Previous studies have demonstrated that the morphology and size of wear debris for the different shape contains a large amount of information, and has the typical fractal characteristics. Such as the edge of wear particle is uneven, rough and non-smooth and the contour curve is continuous, each place of which is not guided. The wear state of the friction pair is complicated and uncertain, but the wear particles have the similar fractal characteristics with a certain degree of regularity. These rules are favorable to study the wear mechanism of friction pair under the different wear conditions (6-9). The traditional characterization methods of wear debris are generally based on the statistical principle and Euclidean geometry, including in area, volume, perimeter, shape factor, surface coefficient and size of long and short axis of the wear debris. Since the shape of wear debris is very different and the profile feature is quite complex, the analytical scale of geometry method has a great influence on the results and the calculation result is not unique (10-13). Some previous researches show that the characterization results of wear debris depend on the Euclidean measurement, and the variation of which can make the characterization to be very instability (14-16). Because the wear debris profile shows a clear fractal feature, the quantitative characterization of wear debris used by the fractal dimension can solve the restricted problem of the traditional measurements.
The common algorithms of wear particle boundary include the size method, box-counting method, variance method, covariance weighted method, spectral dimension method, structural function method and so on (17-20). When calculating the fractal dimension of wear debris boundary, there is an uncertain problem for the size method, box-counting method and variance method. That means that the calculated fractal dimension value may not be unique for a certain boundary. For example, the size method is not only affected by the image factors, but also affected by the calculation method itself, such as the choice of starting point and the step size. Due to the influence of the minimum scale selection and scale interval, the fractal dimension deviation calculated by these methods is very large and the stability is relatively poor. Not only the fractal dimension result is not enough objective, but also the accuracy of fractal dimension cannot be estimated. The covariance weighted method was used to calculate the fractal dimension and the calculated deviation was very small (18,19). Liu Hongtao used the radar map to characterize the wear particles and calculate the fractal dimension, providing a simple and effective calculation method for wear particle profile (20). In this paper, an improved fractal method of radar map is used to investigate the fractal dimension and size distribution of ultra-high-molecular-weight polyethylene (UHMWPE) wear particles in condition of artificial knee joint simulator. The fractal dimension of large gradient for the wear debris with different morphologies can be obtained by this method, which may well distinguish the wear debris morphology and have enough numerical gradients to avoid the effects of errors.
Fractal method of radar graph
Fractal method
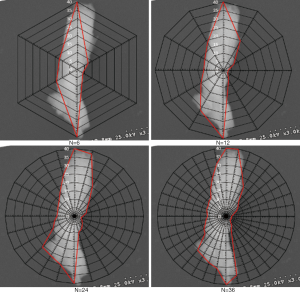
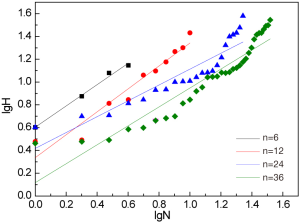
When the wear particles are characterized by the radar graph, the measurement parameters and fractal results are unique. In order to emphasize the influence of degree sequence on the characterization of wear particles, the strip wear debris was selected as an example to draw the radar graph with the decomposing degree value (N) of 6, 12, 24 and 36 respectively, as shown in Figure 1. At the lower value N of 6, there is a large difference between the characteristic boundary image of radar graph and the actual wear debris. With an increase of the decomposing degree value of N, the radar graph is more and more close to the real contour of wear particle. The characterization of the radar graph fractal method at these four decomposing degree values is shown in Figure 2. With the increase of the decomposing degree value, the dispersion degree of the log-log points is weakened, and the slope stability of fitted straight lines is obviously enhanced.
The fractal method of the radar graph proposed by Liu (20) was improved in this paper. The improved radar graph method take each pixel-point at the current resolution of images as an edge point, which is equivalent to selecting the maximum value of indexing sequence of the current image quality. The result error caused by the low value of decomposing degree is overcome by this fractal method. The wear debris fractal method is adopted to extract the boundary coordinates of each debris image and run the iterative calculation to find the maximum relative distance of two coordinate points. The longest axis is determined and then finds the midpoint coordinates of the longest axis, which is confirmed as the image center “O”. Each coordinate point in outline is connected from the beginning of image center in the form of radiation and records its distance to the center as li. And then, all of the values of li are arranged in order of size. The logarithm of the distance value li and ordinal value N (N=1, 2, 3, ···, n) are taken to put into the double logarithmic coordinate system and the corresponding curves of the two values is obtained. According to the following equation, the fractal dimension (D) can be calculated from the slope (α) of log-log plot.
Image processing operation and computer realization
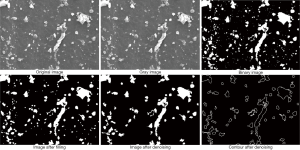
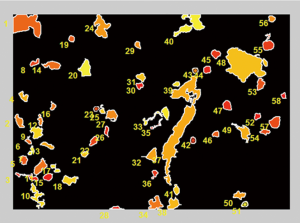
Matlab software is used to write the program to achieve the fractal characterization and size calculation of the wear debris (21-26). The computer image processing includes the binary processing of original picture, internal filling of every single wear debris objects, removing the noises etc. The image processing process is shown in Figure 3. Finally, the outline coordinates of each wear particles are saved to the TXT document according to their labels. In order to carry out fractal characterization of wear debris contour, it is necessary to separate firstly the debris outline from the background in the image. The second step is to take wear debris image to the binary processing by using the suitable gray threshold. The third is to divide image into a number of regions by checking the connectivity of each pixel and its neighboring pixels. The last step is to use the edge detection method to get the boundary outline of each debris objects. Thus each wear debris contour has a unique mark, which can be extracted by their labels shown in Figure 4. The fractal dimension and longest axis size distribution of the single wear debris object can be calculated respectively.
Experimental methods
In this experiment, the artificial joint prosthesis materials of forged CoCrMo and UHMWPE were selected as the commercially available artificial joint implants. The nominal composition of CoCrMo alloy (ISO5832-12) is about 28.2% Cr, 5.98% Mo, 0.41% Ni, 0.70% Fe, 0.64% Mn, 0.23% C, and balance Co (wt%). Mechanical properties of the yield and tensile strength are 590MPa and 840MPa, respectively. Elongation of the forged CoCrMo alloy is about 17.5%. The molecular weight and density of UHMWPE (ISO5834-2) is about 3×106 g/mol and 0.935 g/cm3. The ultimate tensile strength and tensile strength is about 58 and 23 MPa, respectively.
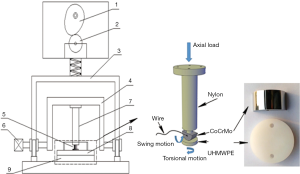
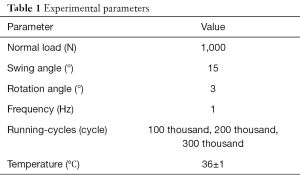
The schematic diagram of the knee joint simulator was produced by University of Leeds (Simulation Solutions Ltd.) (27,28) is shown in Figure 5. The upper sample is CoCrMo alloy and the lower sample is UHMWPE disc. The relevant test parameters are first input into the computer. The servo motor is controlled by the I/O module to drive the cam so that the cantilever moves downward. When the upper specimen of CoCrMo articular head drops in contact with the UHMWPE disc, a contact load of 1,000 N is applied in test. The swing arm controls the swing forward and backward of the upper specimen and the rotation of the lower specimen is controlled by the rotating table. Thus, the compound abrasion motion of the swing and rotation is realized in this experiment. Detailed experimental parameters are shown in Table 1. The simulated body fluid (SBF) was selected to the lubrication media, which was according to the preparation formula proposed by Kokubo (29). The wear debris extraction was based on ISO17853. Scanning electron microscope (Hitachi, S3000N)was used to observe the morphology characteristics of debris.
Full table
Results and discussion
Morphological characteristics of typical wear debris
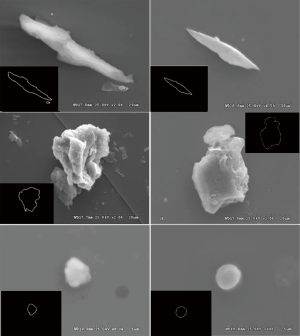
Due to the complexity of the friction motion, the morphology of wear debris shows the different shape and size. According to the profile and surface texture features of wear debris, UHMWPE wear debris can be divided into the strip, needle, flaky, blocky, ellipsoidal and near-spherical wear particles etc. The analysis shows that the larger size of wear debris has more complicated surface morphology. The outline of smaller wear debris gradually becomes near-spherical shape. The typical morphological features of UHMWPE wear particles are shown in Figure 6.
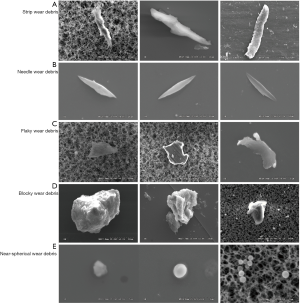
Figure 6A is a typical morphology of the strip wear debris. The appearance of this kind of wear debris is long strip or rod-shaped and the length is more than 3 times the width. The plastic deformation texture can be observed on the surface of the strip wear debris. The particle size is generally about tens of micrometer and a few of wear debris is more than 100 µm in length. The strip wear debris mainly produced in the running-in period due to scratching or rubbing repeatedly on the friction surface of UHMWPE. The ploughing wear is the main reason for the strip wear debris. The morphological feature of the needle wear debris is shown in Figure 6B. It can be seen that the both ends of this kind of debris is like fine needle shape and the middle is thicker. The ratio of width to length is smaller and the particle size is smaller, generally below 20 µm. The boundary of this needle wear debris is very smooth and has less surface roughness with almost no textures or scratches. Because of the smaller size and higher accumulation frequency, the aggregates of needle wear debris are usually visible. It is preliminarily considered that most of the wear particles are produced in steady wear state, and the fatigue spalling is the main reason.
The morphological characteristic of the flaky wear debris is shown in Figure 6C. The plane size distribution of this kind of flaky wear debris is relatively wide with about 20–100 µm. The ploughing wear is found on the surface of part of wear particles, which are the typical fatigue wear products. Due to its small thickness, it is easy to break into small particles under the external force. Under the action of the cyclic load, the wear surface is continuously pressed and deformed. When the local contact stress on the wear surface reaches the yield limit of material, the plastic flow occurs and the micro cracks form in wear subsurface. As a result of the crack propagation, the wear surface material is peeled off to form the flaky wear debris with a larger plane size. As can be seen from SEM pictures in Figure 6D, the blocky wear debris show the irregular shape with the uneven surface and complex texture. Compared with the flaky wear particles, the length and width of blocky wear particles are relatively small. The formation process of blocky wear debris is complex and the particle size is about tens of microns. This kind of wear particles is usually produced by the adhesive wear. Some of them are the wear material spalling at the local region with the weak mechanical properties on the action of shear stress.
The typical SEM morphology of ellipsoidal and near-spherical wear debris is shown in Figure 6E. The geometric contour feature of this wear debris is similar to the spherical shape with the small size. Most of the wear particles are less than 5 µm. The presence of the near-spherical wear debris group was found in sample made of lubricating fluid, which accords with the lowest principle of energy. According to material mechanics theory, the wear particle breakage is the result of frictional shearing stress. When the plane size is much larger than the thickness dimension, there has the advantage of breaking in the vertical plane under the same shear stress. When the plane size is close to the thickness, the contour of wear particle will be approximately spherical. Because the particle size of wear particle is close to the thickness, there is no mechanical priority in the 3D profile of wear particle crushing, and the wear particles are in a relatively stable state of existence. It can be seen from Figure 6E that the boundary and surface of near-spherical wear debris is very smooth and almost no texture was found on the surface. It is considered that this kind of wear debris usually comes from the stable wear stage. Most of them are formed by crushing and rolling the large abrasive particles, which is the typical wear debris related to the movement of friction pair.
Fractal dimension of typical wear debris
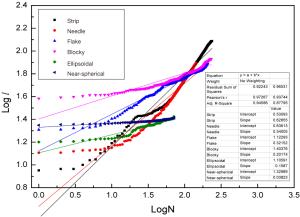
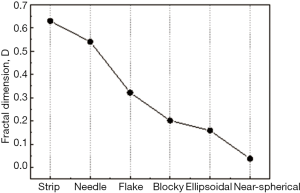
Based on the automatic extraction and fractal recognition program of wear debris, the contour edge recognition and corresponding outline drawing of typical wear debris are shown in Figure 7. By using the improved radar graph method, the fractal curve of different wear particles shown in Figure 8 is obtained. The solid line in the Figure 8 is the fitting line of least-square method. The slope α of the regression line is the fractal dimension D of radar graph. Figure 9 shows the radar graph fractal dimension of UHMWPE wear debris with the different profiles. The results reveal that the fractal feature of the wear debris contour is very obvious. As the debris passes from a larger size of strip wear debris to a smaller size of near-spherical wear debris, the fractal dimension D of the radar graph decrease continuously. According to the characterization of radar graph method, the fractal dimension D is close to zero for the ideal spherical wear debris. It can be seen that the contour curve of wear debris has the independence of size, which can be used as the description parameter of the wear debris contour.
Fractal dimension of wear debris group
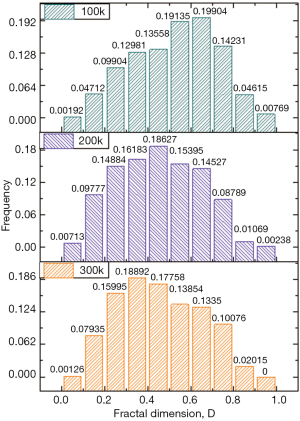
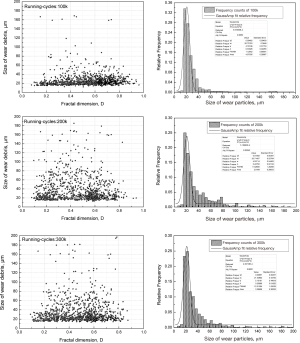
Based on the improved radar graph fractal method, the group fractal identification of ultra-high molecular weight polyethylene debris produced by the different wear test cycles has been carried out in this paper. The fractal dimension D of wear debris in each running cycle is divided into 10 ranges at the range 0 to 1, and the interval is 0.1. Due to the very small case of D >1, it will be incorporated into [0.9, 1.0] interval. The analysis results of fractal dimensions for wear debris groups are shown in Figure 10. The experimental periods are 100 thousand, 200 thousand and 300 thousand running cycles, respectively. When the experimental period is 100 thousand running-cycles, the proportion of strip wear debris with the fractal dimension in 0.6–1.0 reaches for 39.52% of the total wear debris. Secondly, the numbers of the flaky wear debris with the fractal dimension in 0.3–0.5 is about 26.54% of the total wear debris. The fractal dimension of the blocky wear debris is between 0.2–0.3, which accounts for about 9.90% of the total number of wear debris. The fractal dimension of ellipsoidal or near-spherical wear particles is in the range of 0–0.2, and the number of particles is less than 5.0% of the total number of wear particles. Because of the short running-cycles, the friction and wear state is in the running-in period. The wear particles mainly due to the adhesive wear and ploughing wear of the frictional pair. The strip and needle wear debris is the typical morphological characteristics, the proportion of which reaches about 66% of the total wear debris. When the experimental period reaches up to 200 thousand running-cycles, the percentage of the strip wear debris decrease to about 25.24%. But the proportion of flaky wear debris increases to about 34.81%. At the same time, the numbers of blocky and near-spherical wear debris increases to 14.88% and 10.49%, respectively. When the testing period increases to 300 thousand running-cycles, the proportion of strip wear debris does not change any more. The proportion of flaky wear debris continues to increase to about 36.65%. The proportion of needle wear debris decreases to about 13.85%. The percentages of blocky and near-spherical wear debris are almost unchanged. It is found that the friction and wear state has entered a stable wear stage, and the percentages of wear particles with the different fractal dimensions have been in steady state of fluctuation.
With the increase of the experimental running-cycles, the fractal dimension D of wear debris group moves toward the low value direction (Negative shift), and the number of wear debris with the low fractal dimension has an increasing trend. The change of fractal dimension directly reflects the variation characteristics of wear debris shape, which can further deduce the transformation trend of wear mechanism. When the testing period is less than 100 thousand running-cycles, the strip and flaky wear debris with the larger fractal dimension occupy the largest proportion in total wear debris. The adhesive and ploughing wear are the main wear mechanisms in the relevant wear stage, which corresponds to the running-in stage of the friction and wear movement. As the experimental period increased to 200 thousand running-cycles, the proportion of the strip wear debris reduces by about 15%. But the percentages of flaky, blocky and near-spherical wear debris increase obviously. This result reveals that the adhesive and ploughing wear has tended to weaken constantly, and the wear mechanism gradually changes to the abrasive and fatigue spalling wear. And then the wear movement of the friction pair has entered into the composite wear stage. When the testing period increased to 300 thousand running-cycles, the proportion of all kinds of wear debris do not changed too much, and the movement of friction pair has been in the stable wear stage.
Size distribution of wear debris group
Figure 11 shows the particle size distribution of UHMWPE wear debris with the different fractal dimension D. Due to the need to exclude the effect of noise on the data, the analysis filters out the pixel values below 30 points. Under the condition of 100 thousand running-cycles, the size of wear debris is mainly distributed in the range of 10–80 µm. More than 90% of the wear debris size is distributed in the range of 10–40 µm, and there is little proportion of wear debris in excess of 80 µm. After 200 thousand running-cycles, the size distribution range of wear debris becomes wider. The proportion of wear debris between 10–40 µm decreases to 68%, the debris between 40–80 µm increases from 8% to 20%, and the ratio of wear debris larger than 80 µm increases in a certain extent. When the testing period is up to 300 thousand running-cycles, the size of wear debris concentrates to small size, the ratio of wear debris larger than 80 µm decreases significantly.
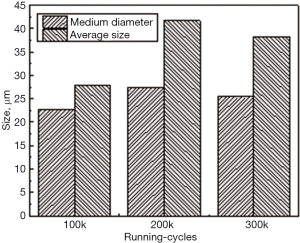
Figure 12 gives the bar graphs for the average size and median diameter (wear particle size with the volume percentage of 50%) of UHMWPE wear debris group. The average particle size and median diameter increase first and then decrease with the increase of wear running-cycles. According to the fractal dimension analysis, it can be considered that this trend of change is corresponding to the evolution of wear process. During the running-in period with shorter wear running-cycles, the joint friction pair is in matching running-in process. The proportion of strip and flaky wear debris with the larger fractal dimension increases with the extension of wear process and the average particle size of wear debris increases. When the friction pair enter the stable wear stage, the matching degree of the joint friction pair tends to be stable and the proportion of various shapes of wear debris has little change. However, the amount of small size wear debris increases due to the fragmentation of larger size wear debris by the action of cyclicing stress, which causes the fractal dimension and average particle size of wear debris group to decrease. Furthermore, the value of median diameter is smaller than that of the average particle size, indicating that although the quantity of larger wear debris is small, the weight of volume percentage can not be neglected. Based on the above analysis, it can be considered that the automatic extraction and fractal identification system of wear debris based on the improved radar graph method can be used for the shape extraction, the fractal dimension calculation and the statistics of wear particle parameters of the single and group of wear debris. It provides a new digital analysis tool for the identification and diagnosis of the artificial joint wear debris.
Conclusions
- The automatic extraction and fractal identification system of wear debris based on the improved radar graph method can be used for the shape extraction, calculation of fractal dimension and statistics of wear particle parameters for the single and group of wear debris. It provides a new digital analysis tool for the identification and diagnosis of the artificial joint wear debris;
- The fractal characteristics of the single UHMWPE wear debris are very obvious. When the wear particles changes from the larger sized strip to the smaller sized near-sphere, the radar fractal dimension decreases continuously. The fractal dimension D of ideal spherical shaped wear debris is close to zero;
- The fractal characteristics of UHMWPE wear debris group directly reflects the transformation trend of wear mechanism. In the initial stage of wear, the strip and flaky wear debris with larger fractal dimension occupy the largest proportion in total wear debris. The adhesive and ploughing wear are the main wear damage mechanisms, corresponding to the running-in stage of the wear movement. With the extension of wear running-cycles, the proportion of strip wear debris reduces and the percentages of flaky and blocky wear debris increase obviously. The wear mechanisms gradually evolve into the abrasive and fatigue spalling wear and the wear movement enters into the composite wear stage. When the friction pair enters the stable wear stage, the proportion of all kinds of wear debris has little change. But the number of small-sized wear debris increases due to the action of cyclic stress, which causes the fractal dimension of wear debris group to decrease to some extent.
Acknowledgments
Funding: This research was supported by National Key Research and Development Program of China (Grant No. 2016YFC1101803) and National Natural Science Foundation of China (Grant No. 51275514, 51575514).
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/aoj.2017.10.11). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Kobayashi A, Bonfield W, Kadoya Y, et al. The size and shape of particulate polyethylene wear debris in total joint replacements. Proc Inst Mech Eng H 1997;211:11-5. [Crossref] [PubMed]
- Goodman SB, Song Y, Yoo JY, et al. Local infusion of FGF-2 enhances bone ingrowth in rabbit chambers in the presence of polyethylene particles. J Biomed Mater Res A 2003;65:454-61. [Crossref] [PubMed]
- Purdue PE, Koulouvaris P, Potter HG, et al. The cellular and molecular biology of periprosthetic osteolysis. Clin Orthop Relat Res 2007;251-61. [Crossref] [PubMed]
- Ge S, Wang Q, Zhang D. Friction and wear behavior of nitrogen ion implanted UHMWPE against ZrO2 ceramic. Wear 2003;255:1069-75. [Crossref]
- Berradja A, Bratu F, Benea L, et al. Effect of sliding wear on tribocorrosion behaviour of stainless steels in a ringer’s solution. Wear 2006;261:987-93. [Crossref]
- Wang A, Sun DC, Yau SS, et al. Orientation softening in the deformation and wear of ultra-high molecular weight polyethylene. Wear 1997;203-204:230-41. [Crossref]
- Ge SR, Wang CT. State-of-the-art and prospect of biotribology in human body. Tribology 2005;25:186-91.
- Liu HT, Ge SR, Luo Y. Multiple fractal of fragmentizing process and distribution of wear particles. Journal of China University of Mining & Technology 2007;36:182-87.
- Song J, Liao Z, Wang S, et al. The research progress on the isolation and characterization for the wear debris of artificial joints. Tribology 2016;36:388-96.
- Minoda Y, Kobayashi A, Iwaki H, et al. Characteristics of polyethylene wear particles isolated from synovial fluid after mobile-bearing and posterior-stabilized total knee arthroplasties. J Biomed Mater Res B Appl Biomater 2004;71:1-6. [PubMed]
- Plumlee K, Schwartz CJ. Investigating UHMWPE wear mechanisms by decomposing wear debris distributions. Wear 2011;271:2208-12. [Crossref]
- McMullin BT, Leung MY, Shanbhag AS, et al. Correlating subjective and objective descriptors of ultra high molecular weight wear particles from total joint prostheses. Biomaterials 2006;27:752-7. [Crossref] [PubMed]
- Liu H, Ge S, Cao S, et al. Comparison of wear debris generated from ultra high molecular weight polyethylene in vivo and in artificial joint simulator. Wear 2011;271:647-52. [Crossref]
- Eckold DG, Dearn KD, Shepherd DET. The evolution of polymer wear debris from total disc arthroplasty. Biotribology 2015;1-2:42-50. [Crossref]
- Liu T, Wood W, Li B, et al. Effect of reinforcement on wear debris of carbon nanofiber/high density polyethylene composites: Morphological study and quantitative analysis. Wear 2012;294:326-35. [Crossref]
- Podsiadlo P, Stachowiak GW. Evaluation of boundary fractal methods for the characterization of wear particles. Wear 1998;217:24-34. [Crossref]
- Zhu H, Ge S. Comparison of fractal characterization effects of structure function and mean square root. Journal of China University of Mining & Technology 2004;33:396-9.
- Ge SR, Suo SF. The computation methods for the fractal dimension of surface profiles. Tribology 1997;17:354-62.
- Chen GA, Ge SR, Wang JX. Application of fractal geometry in tribology. Tribology 1998;18:84-9.
- Liu HT, Ge SR. Description to wear debris boundaries by radar graph fractal method. Chin Sci Bull 2007;52:2285-90. [Crossref]
- Plumlee K, Schwartz CJ. Investigating UHMWPE wear mechanisms by decomposing wear debris distributions. Wear 2011;271:2208-12. [Crossref]
- Roylance BJ, Albidewi IA, Laghari MS. Computer-aided vision engineering (CAVE)-quantification of wear particle morphology. Lubrication Engineering 1994;50:111-6.
- Peng Z, Kirk TB. Automatic wear-particle classification using neural networks. Tribology Letters 1998;5:249-57. [Crossref]
- Gao XQ, Zuo HF, Chen G, et al. Debris image segmentation under complicated background. Journal of Nanjing University of Aeronautics & Astronautics 2001;33:565-8.
- Jia YM, Liu H, Wei HH, et al. Research on the isolation and biological reaction of nano-wear debris from artificial joint. Research Journal of Applied Sciences Engineering and Technology 2013;6:137-43.
- Kowandy C, Mazouz H, Richard C. Isolation and analysis of articular joints wear debris generated in vitro. Wear 2006;261:966-70. [Crossref]
- Chen K, Zhang D, Yang X, et al. Research on torsional friction behavior and fluid load support of PVA/HA composite hydrogel. J Mech Behav Biomed Mater 2016;62:182-94. [Crossref] [PubMed]
- Chen K, Zhang D, Cui X, et al. Research on swing friction lubrication mechanisms and the fluid load support characteristics of PVA–HA composite hydrogel. Tribology International 2015;90:412-19. [Crossref]
- Kokubo T, Takadama H. How useful is SBF in predicting in vivo bone bioactivity? Biomaterials 2006;27:2907-15. [Crossref] [PubMed]
Cite this article as: Chen H, Wang Q, Cui W, Luo Y. Fractal dimension and size distribution characteristics of ultra-high-molecular-weight polyethylene wear particles in condition of artificial knee joint simulator. Ann Joint 2017;2:69.