Computational approaches to study elbow biomechanics
Introduction
Comprehensive knowledge of the in vivo loading environment of the elbow joint is essential in understanding the biomechanical causes associated with elbow diseases and injuries, and in finding appropriate treatments. Computational models can enhance experimental measurements by predicting quantities that cannot be directly measured and by providing insight into the interactions of the different tissues. Computational simulations have become an important tool in understanding ligament injury, tissue damage, and prosthetic design. Computational models of the knee and hip joints have been used extensively, however they have been underutilized in elbow biomechanics. The uncompromised elbow joint is one of the most stable joints in the body through the interactions of bone geometries, ligament constraints, and muscular contractions (1-3). Deficit in any one of these structures can have significant negative effects on normal joint function. The elbow joint is also the most commonly dislocated joint with 49% of these dislocations being complex (dislocation associated with a fracture) which often result in long-term loss of function, chronic stiffness, instability, and post-traumatic osteoarthritis (1,4). Elbow injuries are particularly common in children accounting for at least 10% of all pediatric fractures and are associated with higher complication rates than other common fractures. Children participating in organized sports are also at risk for chronic overuse injuries such as “Little Leaguer’s Elbow” and Osteochondritis Dissecans (5,6). Total elbow arthroplasty was originally used to treat patients with arthritis but as the techniques have evolved, the indications have been expanded to include other disorders and thus the number of elbow replacement surgeries performed is increasing. However, the complication rates remain much higher than arthroplasty of other joints such as the knee and hip (7). Survival rates at ten years for hip and knee replacements are between 94–99% whereas for elbow replacements there is a 27% complication rate and 15-year survivorship is only 70% (7-9). Based on our experience of using computational models for the knee and hip joints, it is easy to see that validated computational models of the elbow joint would be beneficial in addressing some of the aforementioned conditions.
Computational approaches
Finite Element (FE) models
There are two main computational methodologies in biomechanics, the FE method and the Multibody (MB) method. The FE method is a numerical discretization and solution technique that provides a systemic approach for determining the response of complex systems from the individual contributions of the elements (10). The FE method is the ideal approach when studying contact mechanics and tissue deformations of the complex geometries often seen in biomechanics. In elbow biomechanics, one of the first FE models was created by Merz et al. (11) to study the effects of humero-ulnar incongruity. Their model was two-dimensional (2D) and constructed from a plane section through the longitudinal ridge of the trochlear notch following the long axis of the ulna shaft. The cartilage was modeled as a homogeneous isotropic elastic material with a Young’s modulus of 15 MPa. Their FE predictions were compared to experimental measurements using Fuji film. Their model demonstrated bicentric, ventro-dorsal distribution of contact pressure under compressive loads. Wake et al. (12) used a similar 2D FE model to study the mechanism of elbow fracture-dislocations by compressive forces. The FE model was created from a lateral radiograph of a normal elbow. This model included cortical bone, cancellous bone, subchondral bone and cartilage. The cartilage was assigned a constant thickness of 3 mm. All material properties were assumed to by linearly elastic and isotropic. Axial loads were applied at different flexion angles. According to the model, high stress area was concentrated in the coronoid process in low flexion angles and in the base of the coronoid process for flexion angles above 30 degrees. Although this study demonstrated that stress concentration areas depend on the flexion angle, the absence of the radial head and any ligamentous stabilizers restricts the interpretation of the results. Both of the above-mentioned models are 2D thus ignoring any effect of supination-pronation.
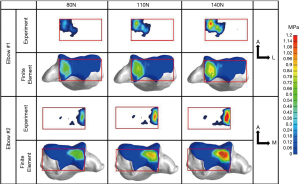
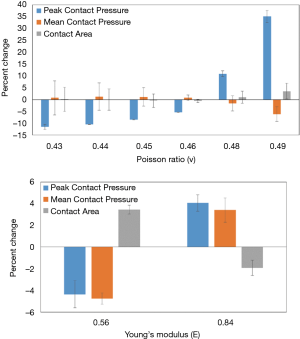
More recently 3D FE models were published by Kim and Carl Miller (13) and Willing et al. (14). Kim and Carl Miller developed a FE model to predict contact stress and contact area of the native humeroradial joint and the predictions were validated using Fuji pressure sensitive film and cadaveric elbows. The 3D model was created from computed tomography (CT) scans of a 46-year-old female cadaveric left elbow at 90 deg flexion and neutral supination/pronation. Bones were modeled as elastic material with Young’s modulus of 400 MPa and Poisson’s ratio of 0.3. Simulations where the bone was modeled as all cortical (orthotropic) material were also examined and compared. Cartilage was modeled as elastic material with Young’s modulus of 10 MPa and Poisson’s ratio of 0.4. Simulations were also run with the cartilage modeled as a neo-Hookean hyperelastic material with shear modulus of 6.8 GPa and compared to the elastic model. Compressive loads of 50, 100, and 200 N were applied on the distal surface of the radial head in the direction of the longitudinal axis. This model also included the annular ligament and the radial collateral ligament modeled as linear springs. Maximum contact stress and contact area in the humeroradial joint predicted by the FE model were within the 95% confidence interval of the measured values. Comparing the choice of bone material produced little difference in those two outcomes. Similarly using hyperelastic versus elastic model for the cartilage produced very little difference in the results. Varying cartilage thickness resulted in 7.5% increase in maximum contact stress and a decrease of 3.5% in contact areas as the thickness of the radial cartilage was reduced from 1.1 to 0.9 mm. Willing et al. used similar methods to model the humero-ulnar articulation. Their 3D FE model was validated experimentally in terms of contact areas determined using a casting method on cadaveric specimens. Cartilage was modeled as neo-Hookean hyperelastic material with varying thickness determined from the medical images. Parametric analyses were performed to evaluate the model’s sensitivity to bone and cartilage material properties and on cartilage thickness geometry. Varying bone material properties had little effect on the predicted contact area and mean contact stress. However, modeling cartilage as a nearly-incompressible material caused a decrease in contact area (30.4%) and an increase in mean contact stress (82.4%). The nearly-incompressible assumption simulates the dynamic response of cartilage (15). The assumption of uniform cartilage thickness had a large effect on contact area. Another study by Renani et al. (16) used magnetic resonance imaging (MRI) derived geometries for the ulna, radius, humerus, and their corresponding cartilages. The FE predictions were compared to experimental measurements using a Tekscan tactile sensor inserted into the joint (Figure 1). Multiple axial loading conditions were performed experimentally and in silico at 20 degrees of elbow flexion. Bones were modeled as rigid bodies and cartilages were modeled as Moony-Rivlin hyperelastic materials. The sensitivity of the FE models to variations of Young’s modulus and Poisson’s ration of the cartilage was also investigated (Figure 2). Peak contact pressure is sensitive to changes in Poisson’s ratio whereas mean contact pressure and contact area are less sensitive. Variation of Young’s modulus resulted in small changes in all outcomes.
All of these studies highlight the areas of importance in elbow FE models. The choice of bone properties results in minimal effects on contact stress and contact areas however, the choice of material properties and uniform cartilage thickness can have significant effects. All elbow FE models developed, investigated static axial compression conditions and there is a need to investigate the effects of load duration, dynamics, and load direction. Soft tissues surrounding the joint are not included in these models and even though they may not affect contact behavior under static loading conditions, including those structures in dynamic conditions may be necessary.
MB models
While FE models are very useful when studying joint stresses and contact areas, they are computationally very expensive and in general have not been used under dynamic conditions. MB models are computationally very efficient and can incorporate muscle dynamics in the formulation of the model. Rigid body dynamic theory forms the foundation for both static and dynamic MB models. Frequently, MB musculoskeletal models are simplified by constraining the degrees of freedom of the joints and disregarding the effects of the ligaments and/or articular contact. Recently, 3D MB models were created where significant advances in overcoming these deficiencies were made. Buffi et al. (17) used a forward dynamics MB model to study muscle, and ligament contributions to elbow varus moment during baseball pitching. Their study demonstrated how important MB models can be in understanding muscle, ligament, and joint interactions during dynamic activities. By increasing the muscle forces they were able to show that the load on the ulnar collateral ligament was reduced. Fisk and Wayne (18) created a model of the elbow and forearm with the joint behavior dictated by articular contact, ligamentous constraints, muscle loading and external perturbations. The musculoskeletal model was constructed by segmentation of the bony geometries from CT scans. Muscles and ligaments were modeled as forces acting along a line of action from origin to insertion points and articular contact was represented by reaction forces applied to the point of contact between the articulating surfaces. Several ligament bundles around the elbow joint and the interosseous membrane were included. Contact forces were computed by applying reaction forces perpendicular to the region of overlap between interfering geometries through a penalty function. The magnitude of the contact force is determined as:
[1]
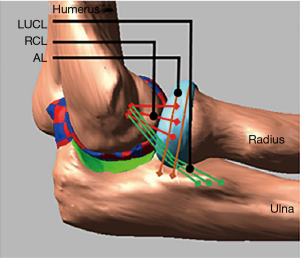
and it depends on the contact stiffness (k), the penetration depth (g), the exponent (e), the penetration velocity and the damping coefficients c and d. The triceps brachii, biceps brachii, and the brachialis insertions were used to apply forces thus inducing elbow flexion. Results were compared to published elbow range of motion data. A similar MB model was used by Spratley and Wayne (19) to study complex varus instability. Validation was conducted by comparing to cadaveric experiments in which the significance of coronoid process fractures, lateral ulnar collateral ligament ruptures, and radial head resection on varus stability was quantified. The MB model accurately reproduced the trends seen in the experiments. Cartilage contact pressure and contact area distributions can be incorporated into a MB model by discretization of the cartilage geometries into smaller rigid bodies and defining contact forces for each of the discrete rigid bodies. This method was demonstrated and validated in knee models (20-27). A similar method was used to investigate the effects of ligament deficiencies on articular contact pressure in the elbow joint (28-30). Another improvement in these models was the incorporation of nonlinear properties for the ligaments (31) and wrapping of the ligaments around the bony structures (Figures 3,4). The nonlinear force-length relationship for ligaments can be described by:
[2]
where k is a stiffness parameter and ϵ is the ligament engineering strain. The spring parameter ϵl is a constant value and assumed to be 0.03 (32). The relation between force and ligament length described above highlights the parabolic transition region from the zero-strain region to the linear region. An extremely important parameter in determining the correct ligament force is the zero-load length of the ligament. Experimental methods on determining this zero-load length have been described in the case of knee ligaments (33), however in the case of the elbow joint these values are not known. Rahman et al. (30) used a similar experimental method to determine those lengths for the lateral ulna collateral, the radial collateral ligament, and the medial collateral ligament.
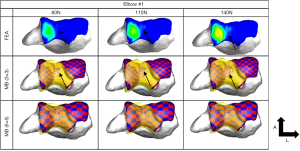
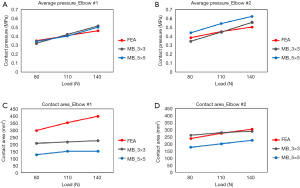
Determination of the appropriate stiffness and exponent values to use in the contact force model is also not established. Rahman et al. (30) used simplified elastic foundation theory to determine the contact stiffness whereas Renani et al. (34) used a previously validated FE model to calibrate the contact force parameters for humerus cartilage discretizations of 3×3 and 5×5 mm cross-sectional areas. The contact parameters were optimized so that the MB model predicted contact pressure was in agreement to the FE model. The study indicated that it is possible to accurately predict contact pressure and contact areas if the discretization is sufficiently small and with the proper choice of parameters (Figures 5,6). MB models employing similar methods in terms of ligament representation have been deployed to study posteromedial rotatory instability in coronoid and ligament deficient elbows (35,36). The predictive ability of these models was demonstrated by comparison to experimental data and to known clinical conditions.
Currently MB models are capable of concurrent prediction of ligament, and articular contact forces and can be used to explore elbow joint behavior under different dynamic loading scenarios and ligament deficient conditions. Understanding the effects of muscle forces on ligament and contact forces is important, especially when studying injury biomechanics. This necessitates resolution of the muscle redundancy problem. Simply stated, muscle redundancy means that there are more unknown muscle forces than equations available from rigid body MD dynamics, leading to an infinite number of muscle solutions for a specific activity. There are primarily three approaches to solving the muscle redundancy problem: optimization methods, electromyography (EMG) driven methods, or reduction of the problem into a muscle length tracking problem and using a controls systems approach. All of these methods have been used in models of the lower extremity successfully (26,27,37-42) but concurrent muscle, ligament, and contact force simulations in the elbow joint are scarce (43). In the study of baseball pitching biomechanics by Buffi et al. (17) used computed muscle control algorithm (38) which is an optimization approach, while Rahman et al. (43) used a controls approach to simulate bicep curls.
Discussion
Imagine a world where orthopaedic interventions, surgical planning and execution are custom tailored to the patient using patient-specific computational models. These models will take into account the individual patient’s bone and soft tissue geometries, movement, expected outcome and long-term goals and through simulation can determine the best treatment options. Computational models are at the forefront of creating such a future. Models can be used in treatment planning by providing an objective method to evaluate treatment options. As computer algorithms and computing power continue to improve, models of increasing complexity can be created that can incorporate elements from both the FE and MB approach. For example, deformable bodies can be implemented in the MB framework by using modal analysis. It is even possible to created workflows where muscle and ligament forces along with kinematics from a MB simulation can be used as boundary and loading conditions to an FE model if detailed stress and strain analysis is necessary. Model validation is a significant barrier in accepting model use in clinical practice (44). Most FE elbow models have been evaluated under static conditions and constant muscle forces, and most MB models have been validated in terms of kinematics. A concerted effort among the modeling community is necessary to advance elbow models to the same level of relevance as other joints (knee and hip). In the case of knee models the ASME Grand Challenge Competition to Predict in Vivo Knee Loads (44,45) provided a comprehensive data set from which different modeling approaches could be validated for accuracy in terms of predicting the in vivo loads on an instrumented knee prosthesis under various dynamics conditions. Competitors used a variety of methods to deal with muscle redundancy, contact, and ligament forces. Teams used static and dynamics optimization, proportional-integral-derivative (PID) control, and EMG driven models to determine muscle forces. In terms of contact forces, deformable models (FE) and elastic foundation models were used, while others used simpler penalty methods. A similar rigorous approach to model validation needs to happen in the case of elbow models to increase clinical applicability.
Acknowledgments
Funding: None.
Footnote
Conflicts of Interest: The author has completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/aoj.2020.04.01). The author has no conflicts of interest to declare.
Ethical Statement: The author is accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Morrey BF. The Elbow and Its Disorders. 3rd edition. W.B. Saunders, 2000.
- Morrey BF, An KN. Functional anatomy of the ligaments of the elbow. Clin Orthop Relat Res 1985.84-90. [Crossref] [PubMed]
- Regan WD, Korinek SL, Morrey BF, et al. Biomechanical study of ligaments around the elbow joint. Clin Orthop Relat Res 1991.170-9. [Crossref] [PubMed]
- Hildebrand KA, Patterson SD, King GJ. Acute elbow dislocations: simple and complex. Orthop Clin North Am 1999;30:63-79. [Crossref] [PubMed]
- Crowther M. Elbow pain in pediatrics. Curr Rev Musculoskelet Med 2009;2:83-7. [Crossref] [PubMed]
- Takahara M, Mura N, Sasaki J, et al. Classification, treatment, and outcome of osteochondritis dissecans of the humeral capitellum. J Bone Joint Surg Am 2007;89:1205-14. [Crossref] [PubMed]
- Sanchez-Sotelo J. Total elbow arthroplasty. Open Orthop J 2011;5:115-23. [Crossref] [PubMed]
- Milošev I, Kovac S, Trebse R, et al. Comparison of ten-year survivorship of hip prostheses with use of conventional polyethylene, metal-on-metal, or ceramic-on-ceramic bearings. J Bone Joint Surg Am 2012;94:1756-63. [Crossref] [PubMed]
- Kremers HM, Sierra RJ, Schleck CD, et al. Comparative Survivorship of Different Tibial Designs in Primary Total Knee Arthroplasty. J Bone Joint Surg Am 2014;96:e121. [Crossref] [PubMed]
- Maas SA, Ellis BJ, Ateshian GA, et al. FEBio: finite elements for biomechanics. J Biomech Eng 2012;134:011005. [Crossref] [PubMed]
- Merz B, Eckstein F, Hillebrand S, et al. Mechanical implications of humero-ulnar incongruity--finite element analysis and experiment. J Biomech 1997;30:713-21. [Crossref] [PubMed]
- Wake H, Hashizume H, Nishida K, et al. Biomechanical analysis of the mechanism of elbow fracture-dislocations by compression force. J Orthop Sci 2004;9:44-50. [Crossref] [PubMed]
- Kim S, Carl Miller M. Validation of a Finite Element Humeroradial Joint Model of Contact Pressure Using Fuji Pressure Sensitive Film. J Biomech Eng 2016;138. [Crossref] [PubMed]
- Willing RT, Lalone EA, Shannon H, et al. Validation of a finite element model of the human elbow for determining cartilage contact mechanics. J Biomech 2013;46:1767-71. [Crossref] [PubMed]
- Ateshian GA, Ellis BJ, Weiss JA. Equivalence between short-time biphasic and incompressible elastic material responses. J Biomech Eng 2007;129:405-12. [Crossref] [PubMed]
- Renani MS, Rahman M, Cil A, et al. Ulna-humerus contact mechanics: Finite element analysis and experimental measurements using a tactile pressure sensor. Med Eng Phys 2017;50:22-8. [Crossref] [PubMed]
- Buffi JH, Werner K, Kepple T, et al. Computing muscle, ligament, and osseous contributions to the elbow varus moment during baseball pitching. Ann Biomed Eng 2015;43:404-15. [Crossref] [PubMed]
- Fisk JP, Wayne JS. Development and validation of a computational musculoskeletal model of the elbow and forearm. Ann Biomed Eng 2009;37:803-12. [Crossref] [PubMed]
- Spratley EM, Wayne JS. Computational model of the human elbow and forearm: application to complex varus instability. Ann Biomed Eng 2011;39:1084-91. [Crossref] [PubMed]
- Guess TM, Stylianou A. Simulation of anterior cruciate ligament deficiency in a musculoskeletal model with anatomical knees. Open Biomed Eng J 2012;6:23-32. [Crossref] [PubMed]
- Guess TM. Forward Dynamics Simulation Using a Natural Knee with Menisci in the Multibody Framework. Multibody Syst Dyn 2012;28:37-53. [Crossref]
- Paiva G, Bhashyam S, Thiagarajan G, et al. A data-driven surrogate model to connect scales between multi-domain biomechanics simulations. Annu Int Conf IEEE Eng Med Biol Soc 2012;2012:3077-80. [Crossref] [PubMed]
- Guess TM, Liu H, Bhashyam S, et al. A multibody knee model with discrete cartilage prediction of tibio-femoral contact mechanics. Comput Methods Biomech Biomed Engin 2013;16:256-70. [Crossref] [PubMed]
- Stylianou AP, Guess TM, Kia M. Multibody muscle driven model of an instrumented prosthetic knee during squat and toe rise motions. J Biomech Eng 2013;135:041008. [Crossref] [PubMed]
- Lu Y, Pulasani PR, Derakhshani R, et al. Application of neural networks for the prediction of cartilage stress in a musculoskeletal system. Biomed Signal Process Control 2013;8:475-82. [Crossref] [PubMed]
- Kia M, Stylianou AP, Guess TM. Evaluation of a musculoskeletal model with prosthetic knee through six experimental gait trials. Med Eng Phys 2014;36:335-44. [Crossref] [PubMed]
- Guess TM, Stylianou AP, Kia M. Concurrent prediction of muscle and tibiofemoral contact forces during treadmill gait. J Biomech Eng 2014;136:021032. [Crossref] [PubMed]
- Rahman M, Cil A, Bogener JW, et al. Lateral collateral ligament deficiency of the elbow joint: A modeling approach. J Orthop Res 2016;34:1645-55. [Crossref] [PubMed]
- Rahman M, Cil A, Stylianou AP. Medial Collateral Ligament Deficiency of the Elbow Joint: A Computational Approach. Bioengineering (Basel) 2018;5:84. [Crossref] [PubMed]
- Rahman M, Cil A, Stylianou AP. Prediction of elbow joint contact mechanics in the multibody framework. Med Eng Phys 2016;38:257-66. [Crossref] [PubMed]
- Blankevoort L, Huiskes R. Ligament-bone interaction in a three-dimensional model of the knee. J Biomech Eng 1991;113:263-9. [Crossref] [PubMed]
- Blankevoort L, Kuiper JH, Huiskes R, et al. Articular contact in a three-dimensional model of the knee. J Biomech 1991;24:1019-31. [Crossref] [PubMed]
- Bloemker KH, Guess TM, Maletsky L, et al. Computational knee ligament modeling using experimentally determined zero-load lengths. Open Biomed Eng J 2012;6:33-41. [Crossref] [PubMed]
- Renani MS, Rahman M, Cil A, et al. Calibrating multibody ulno-humeral joint cartilage using a validated finite element model. Multibody Syst Dyn 2018;44:81-91. [Crossref]
- Terzini M, Zanetti EM, Audenino AL, et al. Multibody modelling of ligamentous and bony stabilizers in the human elbow. Muscles Ligaments Tendons J 2018;7:493-502. [Crossref] [PubMed]
- Karademir G, Bachman DR, Stylianou AP, et al. Posteromedial rotatory incongruity of the elbow: a computational kinematics study. J Shoulder Elbow Surg 2019;28:371-80. [Crossref] [PubMed]
- Thelen DG, Anderson FC, Delp SL. Generating dynamic simulations of movement using computed muscle control. J Biomech 2003;36:321-8. [Crossref] [PubMed]
- Thelen DG, Anderson FC. Using computed muscle control to generate forward dynamic simulations of human walking from experimental data. J Biomech 2006;39:1107-15. [Crossref] [PubMed]
- Zevenbergen L, Smith CR, Van Rossom S, et al. Cartilage defect location and stiffness predispose the tibiofemoral joint to aberrant loading conditions during stance phase of gait. PLoS One 2018;13:e0205842. [Crossref] [PubMed]
- Besier TF, Gold GE, Beaupre GS, et al. A modeling framework to estimate patellofemoral joint cartilage stress in vivo. Med Sci Sports Exerc 2005;37:1924-30. [Crossref] [PubMed]
- Besier TF, Fredericson M, Gold GE, et al. Knee muscle forces during walking and running in patellofemoral pain patients and pain-free controls. J Biomech 2009;42:898-905. [Crossref] [PubMed]
- Guess TM, Razu S, Jahandar H, et al. Predicted loading on the menisci during gait: The effect of horn laxity. J Biomech 2015;48:1490-8. [Crossref] [PubMed]
- Rahman M, Sharifi Renani M, Cil A, et al. Musculoskeletal Model Development of the Elbow Joint with an Experimental Evaluation. Bioengineering (Basel) 2018;5:31. [Crossref] [PubMed]
- Fregly BJ, Besier TF, Lloyd DG, et al. Grand challenge competition to predict in vivo knee loads. J Orthop Res 2012;30:503-13. [Crossref] [PubMed]
- Kinney AL, Besier TF, D'Lima DD, et al. Update on grand challenge competition to predict in vivo knee loads. J Biomech Eng 2013;135:021012. [Crossref] [PubMed]
Cite this article as: Stylianou A. Computational approaches to study elbow biomechanics. Ann Joint 2021;6:11.